Equazione della retta: formule ed esempi
Informazioni sul documento
| Lingua | Italian |
| Formato | |
| Dimensione | 665.80 KB |
Riassunto
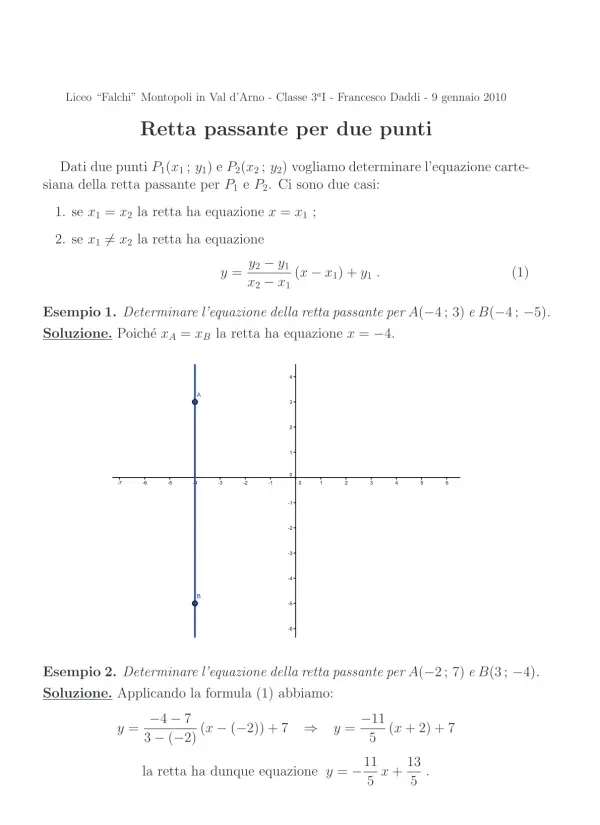
I.Equazione della retta passante per due punti
Questa sezione si concentra sul calcolo dell'equazione di una retta noti due punti. Vengono illustrate le metodologie per determinare l'equazione cartesiana di una retta, applicando la formula del punto-pendenza e la formula della retta passante per due punti. Si affrontano esercizi pratici sulla determinazione dell'equazione della retta, considerando casi di rette parallele e perpendicolari. Si introduce anche il concetto di coefficiente angolare.
1. Definizione del problema e casi particolari
Il documento inizia introducendo il problema fondamentale: determinare l'equazione cartesiana di una retta passante per due punti, P1(x1; y1) e P2(x2; y2). Si accenna all'esistenza di due casi, sebbene non vengano esplicitati nel testo fornito. Questa introduzione pone le basi per la successiva trattazione pratica attraverso esempi ed esercizi. L'enfasi è posta sulla determinazione dell'equazione della retta, un concetto chiave della geometria analitica, utilizzando le coordinate dei punti dati. La comprensione di questa sezione è fondamentale per affrontare i problemi successivi, che utilizzeranno e svilupperanno ulteriormente i concetti introdotti in questo punto iniziale. L'obiettivo principale è la padronanza della relazione tra i punti nel piano cartesiano e la loro rappresentazione tramite l'equazione della retta che li congiunge. La capacità di individuare l'equazione rappresenta un'abilità fondamentale nella geometria analitica e nella risoluzione di problemi geometrici più complessi.
2. Esercizi applicativi e soluzioni
La sezione successiva presenta esercizi pratici volti a consolidare la comprensione del calcolo dell'equazione di una retta passante per due punti. Un esempio concreto è dato dall'esercizio che richiede di trovare l'equazione della retta passante per A(3; 4) e B(2; 2), con la soluzione fornita: y = 2x - 2. Questo tipo di esercizio, insieme ad altri simili presenti nel documento, permette allo studente di applicare i concetti teorici e di sviluppare la propria capacità di risoluzione di problemi. La presenza di soluzioni permette allo studente di verificare la propria comprensione e di identificare eventuali errori nel processo di calcolo. La ripetizione di esercizi simili, con dati numerici diversi, aiuta a fissare il metodo di risoluzione e ad automatizzare il processo di calcolo dell'equazione della retta. L'obiettivo finale è la capacità di affrontare in modo autonomo problemi simili, utilizzando correttamente le formule e le metodologie illustrate.
3. Rette parallele e perpendicolari nel contesto dell equazione della retta
Sebbene non sia una sezione dedicata esclusivamente a questo aspetto, il documento include esercizi che toccano il tema delle rette parallele e perpendicolari in relazione all'equazione della retta passante per due punti. Ad esempio, si richiede di scrivere l'equazione di una retta parallela ad una retta data e passante per un punto specifico. Questo tipo di esercizio non solo rafforza la comprensione del concetto di equazione della retta, ma anche la relazione tra il coefficiente angolare e la direzione della retta. La capacità di determinare l'equazione di rette parallele e perpendicolari è un'abilità essenziale per risolvere problemi geometrici più complessi, e questi esercizi mirano a sviluppare questa capacità. Si osserva quindi un'applicazione pratica del concetto di coefficiente angolare e del suo significato geometrico all'interno del più ampio contesto della determinazione dell'equazione di una retta.
4. Esercizi di preparazione alla verifica e soluzioni
Il documento presenta una serie di esercizi di preparazione a una verifica, con particolare attenzione al calcolo dell'equazione di una retta. Gli esercizi includono esempi di rette parallele e perpendicolari, richiedendo di scrivere le loro equazioni date opportune condizioni. La presenza di esercizi specifici che includono sia la scrittura dell'equazione di una retta, partendo da due punti, che la costruzione di rette parallele o perpendicolari, sottolinea l'importanza di padroneggiare entrambi i concetti. La sezione delle soluzioni fornisce un ulteriore strumento per l'apprendimento, permettendo allo studente di confrontare il proprio lavoro con quello corretto e di identificare eventuali errori di metodo o di calcolo. Questi esercizi mirano a consolidare le conoscenze e le abilità acquisite, preparando lo studente alla verifica finale.
II.Intersezione di due rette e Asse di un Segmento
Questa parte del documento tratta il problema della determinazione del punto di intersezione di due rette. Vengono forniti esempi ed esercizi svolti sul calcolo delle coordinate del punto di intersezione. Inoltre, si approfondisce il calcolo dell'equazione dell'asse di un segmento, utilizzando la formula della distanza per trovare il luogo geometrico dei punti equidistanti dagli estremi del segmento. Si utilizzano le coordinate cartesiane per risolvere i problemi.
1. Intersezione di due rette
Una sezione significativa del documento è dedicata all'analisi dell'intersezione di due rette. Gli esercizi proposti richiedono di determinare le coordinate del punto di intersezione, partendo dalle equazioni delle due rette. Un esempio concreto mostra due rette, r e s, con equazioni r: y = (1/4)x - 1 e s (non esplicitata nel testo ma deducibile dal contesto). La soluzione evidenzia che le rette sono perpendicolari perché il prodotto dei loro coefficienti angolari è uguale a -1. Questo concetto viene utilizzato per determinare le coordinate del punto di intersezione, dimostrando come la conoscenza del coefficiente angolare e della relazione tra rette parallele e perpendicolari sia fondamentale per la risoluzione del problema. La determinazione del punto di intersezione rappresenta un'applicazione pratica dell'algebra lineare e della geometria analitica, con il piano cartesiano che fornisce il contesto geometrico per la risoluzione del problema. La capacità di risolvere questo tipo di problema è essenziale per affrontare problemi di geometria analitica più complessi.
2. Equazione dell asse di un segmento
Il documento presenta diversi esercizi sulla determinazione dell'equazione cartesiana dell'asse di un segmento, dato dai suoi estremi. Viene proposto l'esercizio di determinare l'equazione dell'asse del segmento con estremi A(2; -3) e B(4; 7), e un secondo esercizio con estremi A(-5; 1) e B(0; -4). La soluzione fornisce la formula generale (x - xA)² + (y - yA)² = (x - xB)² + (y - yB)² per l'equazione cartesiana dell'asse di un segmento. Questo metodo si basa sulla proprietà che l'asse di un segmento è il luogo geometrico dei punti equidistanti dagli estremi del segmento. Attraverso questi esempi, viene mostrato come applicare questa formula per determinare l'equazione dell'asse, sottolineando l'importanza di saper manipolare le equazioni algebriche per arrivare alla forma cartesiana desiderata. La comprensione di questo concetto è essenziale nella geometria analitica e trova applicazione nella risoluzione di problemi geometrici che coinvolgono simmetrie e proprietà di figure geometriche nel piano cartesiano.
3. Applicazione in verifiche e esercizi di preparazione
L'argomento dell'intersezione di rette e dell'asse di un segmento viene ulteriormente esplorato in diverse verifiche e negli esercizi di preparazione. In una verifica scritta, viene richiesto di determinare l'intersezione tra una retta con equazione 5x - 2y = 8 e la retta passante per i punti A(0; 2) e B(3; 0). Questo evidenzia l'importanza della capacità di manipolare equazioni e di determinare le coordinate del punto di intersezione. Un altro esercizio, presente in una verifica orale, richiede di determinare l'equazione implicita dell'asse di un segmento con estremi dati. Queste domande nelle verifiche sottolineano l'importanza di questi concetti nella comprensione più ampia della geometria analitica. La presenza di questi esercizi nelle verifiche, sia scritte che orali, rafforza il ruolo centrale che la determinazione dell'intersezione di rette e dell'equazione dell'asse di un segmento hanno nell'apprendimento della geometria analitica.
III.Punto medio di un segmento e lunghezza di un segmento
Questa sezione si focalizza sul calcolo del punto medio di un segmento tramite la formula del punto medio. Vengono proposti esercizi che richiedono il calcolo delle coordinate del punto medio dato due punti estremi. In aggiunta, vengono trattati esercizi sul calcolo della lunghezza di un segmento nel piano cartesiano usando la formula della distanza tra due punti. Si considera anche la relazione tra la lunghezza del segmento e le coordinate cartesiane dei suoi estremi.
1. Calcolo del punto medio di un segmento
Il documento dedica una parte significativa all'applicazione della formula del punto medio di un segmento. Numerosi esercizi richiedono di calcolare le coordinate del punto medio M di un segmento AB, dati i punti estremi A e B. Ad esempio, in una verifica orale, viene esplicitamente richiesta la formula per il calcolo del punto medio, sottolineando l'importanza di questa formula come strumento fondamentale della geometria analitica. In altri esercizi, il calcolo del punto medio è utilizzato come passaggio intermedio per risolvere problemi più complessi, come la determinazione delle coordinate di un punto B dato il punto medio M e il punto A. Questa applicazione ripetuta in diversi contesti evidenzia l'importanza di padroneggiare il calcolo del punto medio, sia come concetto a sé stante che come strumento per affrontare problemi più complessi. La formula del punto medio, quindi, non è solo un argomento teorico, ma uno strumento operativo fondamentale per la risoluzione di problemi geometrici nel piano cartesiano.
2. Calcolo della lunghezza di un segmento
Un altro aspetto rilevante del documento è il calcolo della lunghezza di un segmento nel piano cartesiano. Diversi esercizi richiedono di determinare la lunghezza di un segmento AB, dati i suoi estremi A e B. Questo calcolo si basa sulla formula della distanza tra due punti nel piano cartesiano, una formula altrettanto importante nella geometria analitica. In alcuni casi, il calcolo della lunghezza del segmento è richiesto come parte di un problema più ampio, come la determinazione del perimetro di un triangolo o la verifica di proprietà geometriche. La capacità di calcolare la lunghezza di un segmento è quindi un'abilità fondamentale, che va oltre la semplice applicazione della formula e che richiede la comprensione del significato geometrico della distanza tra due punti. Il documento sottolinea l'importanza di questa abilità attraverso la sua ricorrenza in diversi esercizi e verifiche, evidenziando la sua centralità nella comprensione della geometria analitica.
3. Relazione tra punto medio e lunghezza del segmento in problemi applicativi
Il documento non solo presenta esercizi isolati sul punto medio e sulla lunghezza di un segmento, ma integra questi due concetti in problemi più complessi. Ad esempio, in un esercizio viene chiesto di trovare le coordinate di un punto B, dato il punto medio M e il punto A. Questo richiede non solo di conoscere la formula del punto medio, ma anche di saperla applicare per risolvere un'equazione a due incognite. In altri esercizi, si richiede di calcolare la lunghezza di un segmento che ha come estremi un punto dato e il punto medio di un altro segmento. Questa integrazione di concetti diversi in un singolo problema dimostra la capacità di applicazione pratica e la comprensione delle relazioni tra diversi elementi geometrici nel piano cartesiano. La capacità di collegare diversi concetti geometrici è un segno di comprensione approfondita e di padronanza delle tecniche di risoluzione dei problemi.
IV.Esercizi sulle rette parallele e perpendicolari
Questa parte presenta numerosi esercizi sulla scrittura dell'equazione di una retta parallela o perpendicolare ad una retta data, passando per un punto specifico. Gli esercizi rafforzano la comprensione dei concetti di coefficiente angolare, rette parallele, e rette perpendicolari e la loro relazione con l'equazione della retta in forma esplicita ed implicita. Si usano le coordinate cartesiane per definire la posizione di punti e rette.
1. Determinazione di rette parallele
Una parte significativa degli esercizi si concentra sulla capacità di determinare l'equazione di una retta parallela ad una retta data, passante per un punto specifico. Questo implica la comprensione del concetto di coefficiente angolare: rette parallele hanno lo stesso coefficiente angolare. Gli esercizi richiedono di applicare questa conoscenza per trovare l'equazione della retta parallela, utilizzando la forma punto-pendenza o altre forme equivalenti dell'equazione della retta. Un esempio tipico è quello di trovare l'equazione di una retta parallela a y = 2x + 6 e passante per il punto P(-5; 4). La soluzione di questi esercizi richiede non solo di conoscere la definizione di rette parallele, ma anche di saperla applicare in modo pratico per determinare l'equazione della retta richiesta, dimostrando la capacità di utilizzare le informazioni date per costruire l'equazione corretta. Questo aspetto è fondamentale nella geometria analitica e trova applicazione in diversi contesti.
2. Determinazione di rette perpendicolari
Il documento include anche esercizi che affrontano la determinazione dell'equazione di una retta perpendicolare ad una retta data, passante per un punto specifico. In questo caso, la relazione tra i coefficienti angolari è fondamentale: il prodotto dei coefficienti angolari di due rette perpendicolari è -1. Gli esercizi richiedono di applicare questa relazione per determinare il coefficiente angolare della retta perpendicolare e, successivamente, di utilizzare la forma punto-pendenza o altre forme equivalenti per scrivere l'equazione completa. Ad esempio, un esercizio chiede di trovare una retta perpendicolare a y = (3/4)x - 3. La risoluzione di questi esercizi dimostra la comprensione del concetto di perpendicolarità tra rette e la sua traduzione in termini algebrici. La capacità di manipolare le equazioni e di applicare le proprietà geometriche è essenziale per la risoluzione di problemi geometrici nel piano cartesiano.
3. Esercizi combinati e applicazioni in contesti più ampi
Alcuni esercizi richiedono di combinare la conoscenza delle rette parallele e perpendicolari con altri concetti della geometria analitica. Ad esempio, un esercizio potrebbe richiedere di trovare l'equazione di una retta parallela ad una retta passante per due punti dati, o di trovare l'equazione di una retta perpendicolare ad un segmento dato. Questi esercizi più complessi mettono alla prova la capacità di integrare diverse conoscenze e di applicare le formule in contesti più ampi. La presenza di questi esercizi indica l'importanza di non considerare la conoscenza delle rette parallele e perpendicolari in modo isolato, ma di integrarla con altri concetti della geometria analitica per la risoluzione di problemi più sfidanti. Questo approccio rafforza la comprensione globale dei principi della geometria analitica e migliora la capacità di problem solving.
V.Circonferenza e sue proprietà
Questa sezione introduce brevemente l'equazione di una circonferenza, specificatamente nel caso in cui il diametro sia un segmento dato. Si utilizza il punto medio del segmento come centro della circonferenza e la metà della lunghezza del segmento come raggio. Si sfrutta la conoscenza del punto medio e della distanza per ricavare l'equazione.
1. Il centro della circonferenza con diametro AB
Una domanda all'interno di una verifica orale riguarda la posizione del centro di una circonferenza che ha come diametro il segmento AB. Le opzioni di risposta sono multiple: il punto medio di AB, il punto A, il punto B, oppure 'non è possibile stabilirlo'. Questa domanda non richiede il calcolo dell'equazione della circonferenza, ma la comprensione di una proprietà geometrica fondamentale: il centro di una circonferenza costruita su un diametro si trova nel punto medio del diametro stesso. La corretta risposta è il punto medio di AB. Questa domanda, sebbene semplice, testa la conoscenza di un concetto geometrico di base applicato alle circonferenze, mostrando come la conoscenza di proprietà geometriche sia integrata con la comprensione delle coordinate nel piano cartesiano. La scelta multipla permette una verifica rapida e precisa della conoscenza.
2. Equazione della circonferenza dato il diametro
Un altro esercizio, sempre all'interno di una verifica orale, richiede la determinazione dell'equazione della circonferenza avente come diametro il segmento AB, dove A(1; 1) e B(-1; -1). Le opzioni di risposta sono equazioni di circonferenze con centri diversi e raggi diversi. Questa domanda richiede una comprensione più approfondita, che include non solo la conoscenza della posizione del centro (punto medio del diametro), ma anche il calcolo del raggio (metà della lunghezza del diametro) per poter scrivere correttamente l'equazione della circonferenza. La soluzione dell'esercizio richiede l'applicazione della formula dell'equazione della circonferenza, combinata con il calcolo del punto medio e della distanza tra due punti. Questo esercizio dimostra che la comprensione della geometria delle circonferenze va di pari passo con la capacità di applicare le formule e le conoscenze di geometria analitica.
3. Derivazione dell equazione di una circonferenza da proprietà geometriche
Una parte del testo mostra un esempio di come derivare l'equazione di una circonferenza sfruttando le sue proprietà geometriche. Partendo dalla considerazione che il centro della circonferenza si trova nel punto medio del segmento AB (diametro), e che il raggio è la metà della lunghezza di AB, si procede al calcolo dell'equazione. Il testo mostra un esempio numerico con coordinate specifiche, arrivando all'equazione finale semplificata. Questo esempio illustra come la conoscenza di concetti geometrici fondamentali, come il punto medio e la lunghezza del segmento, possa essere utilizzata per determinare l'equazione di una circonferenza. La semplificazione dell'equazione finale sottolinea l'importanza della padronanza delle tecniche algebriche per ottenere una rappresentazione più concisa ed elegante della circonferenza nel piano cartesiano. Questo metodo evidenzia il legame tra geometria e algebra nella geometria analitica.
VI.Verifiche e Applicazioni
Il documento include diverse verifiche scritte e orali, con domande che testano la comprensione dei concetti di equazione della retta, punto medio, distanza tra due punti, intersezione di rette, e altre proprietà geometriche nel piano cartesiano. Le verifiche utilizzano diversi formati di domande, tra cui a risposta multipla e problemi aperti, per valutare la comprensione degli argomenti trattati.
1. Verifiche Orali Domande a risposta multipla e problemi aperti
Il documento include diverse verifiche orali con domande a risposta multipla e problemi aperti. Le verifiche orali presentano domande che richiedono la conoscenza di concetti chiave come il calcolo del punto medio di un segmento, l'equazione della retta passante per due punti, e la posizione del centro di una circonferenza dato il suo diametro. Il sistema di punteggio prevede un punteggio di partenza e un punteggio per ogni risposta corretta, errata o lasciata in bianco. Le domande a risposta multipla verificano la conoscenza di concetti specifici, mentre i problemi aperti richiedono una maggiore capacità di applicazione delle formule e di ragionamento geometrico. Le verifiche orali rappresentano un metodo di valutazione che testa sia la conoscenza teorica che la capacità di applicare i concetti in modo rapido e preciso.
2. Verifiche Scritte Esercizi di applicazione pratica
Le verifiche scritte includono esercizi più complessi che richiedono l'applicazione pratica dei concetti studiati. Ad esempio, si richiede di determinare l'equazione di una retta passante per due punti dati, l'intersezione di due rette, le coordinate di un punto dato il punto medio e un altro estremo, e la distanza tra un punto e una retta. Ogni esercizio ha un punteggio assegnato, e per ottenere la sufficienza è necessario dimostrare una comprensione adeguata dei concetti base, in particolare in relazione alle rette. Questi esercizi scritti consentono una valutazione più approfondita della comprensione e dell'abilità di applicare i concetti in modo autonomo, richiedendo una maggiore elaborazione e giustificazione delle risposte rispetto alle domande a risposta multipla delle verifiche orali.
3. Esercizi di Preparazione Consolidamento dei concetti chiave
Il documento comprende una serie di esercizi di preparazione alle verifiche, mirati a consolidare i concetti chiave della geometria analitica. Questi esercizi coprono un'ampia gamma di argomenti, tra cui il calcolo del punto medio e della lunghezza di un segmento, la determinazione dell'equazione di una retta (comprese rette parallele e perpendicolari), e l'individuazione del punto di intersezione tra due rette. La presenza di una sezione dedicata alle soluzioni permette agli studenti di autovalutare la propria comprensione e di individuare eventuali lacune nella propria preparazione. Questi esercizi servono come strumento di apprendimento attivo, permettendo agli studenti di applicare e consolidare i concetti teorici in modo autonomo, prima di affrontare le verifiche formali. Questa fase di preparazione è cruciale per assicurare una comprensione solida e una maggiore sicurezza durante le verifiche.
